 Essen, horizontal view
Essen, horizontal view
|
Internet Project
Observing, Photographing and Evaluating the
Transit of Venus, June 8th, 2004
|
 Essen, equatorial view
Essen, equatorial view
|
Project 6: The Transit of Mercury on May 7th, 2003
On May 7th, roughly between 5.15 UT and 10.40 UT, a Mercury transit will
happen, that means Mercury will cross the sun's disc. Because of the
geometrical circumstances to be very similar to those of the Venus transit in
June 2004 this event offers an excellent occasion to exercise observing,
photographing and measuring a transit.

|
|

|
|
Animation of Merkur's transit (M. Federspiel)
|
|
Merkury's positions between 5.30 UT and 11.30 UT,
"recorded" every 15 minutes from Essen
|
The main ideas of this project are the following:
- We will photograph Mercury in front of the sun in the same manner
as we will do with Venus next year.
- To be able to derive the distance to the sun (see the related paper, up to now only in German)
we will try to get exact positions of Mercury relative to the sun's
disc simoultaneously taken from as many different places of the world as
possible.
- Instead of taking just one position we will track the whole pass of
Mercury across the sun because
- there may occur obstacles (clouds, for instance) to photograph exactly at
the same time and
- the parallax effect may be too small to be measured by comparing only two
pictures.
In this way we hope to become able to apply statistical methods (Gauss' mean
square method) to calculate simultaneous positions.
Method of photographing and evaluating
- Take photographs of Sun and Mercury all 15 minutes, if possible
exactly at 5.30 UT, 5.45 UT, 6.00 UT and so on until 10.30 UT. To be
able to determine Mercury's position the whole sun should be on the picture.
- On every picture, there must be determined
- the center M of the sun's disc,
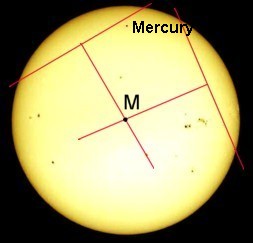
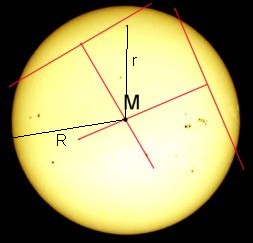
- the radius R of the sun's disc (in millimeters or
pixels),
- the distance r of Mercury from M (in
millimeters or pixels, too),
- the direction to north (The best method for this may be to
exposure each picture twice without tracking the telescope; the sun then
will move by its own diameter in about 130 seconds. If the camera
doesn't offer this possibility it may also be suitable to make everytime two
different pictures and to compare the sun's positions on both.)
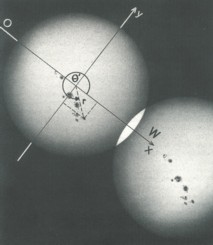
- and the position angle Θ' measured relative to
west.
- To make comparisons possible between pictures of different scale use the
relative distance r'=r/R instead of its
absolute value r.
- Distance r' and position angle Θ'
are to be transformed into rectangular coordinates:
x' = r'cosΘ'
y' = r'sinΘ'
- By using Gauss' mean square method these values can be fitted to a line:
x'(Δt) = x0'(t0) + a(Δt)
y'(Δt) = y0'(t0) + b(Δt)
Here, t0 means 8.00 UT and Δt
means the time difference to t0
(Δt<0 means before 8.00 UT).
A typical table of results may look like the following (You can download an
appropriate Excel worksheet here!):
| Name
|
| geogr. position
|
| Time (UT) | Δt in s | r'=r/R
| pos. angle Θ'
| x'=x/R | y'=y/R
|
| 5.30 | -9000 | | | |
|
| 5.45 | -8100 | | | |
|
| 6.00 | -7200 | | | |
|
| .............
|
| 8.00 | 0 | | | |
|
| .............
|
| 10.30 | 9000 | | | |
|
- Additionally, we should try to measure the exact time for the first,
second, third and forth contact of Mercury:
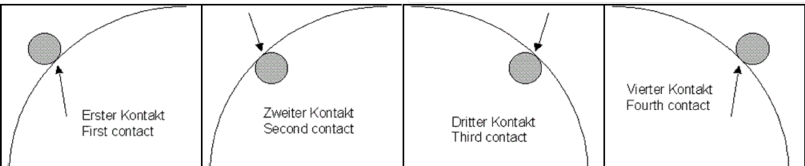
Perhaps, we will try to derive the distance to the Sun by comparing different
transit durations measured at different locations. This method was
historically proposed by E. Halley and used for the evaluation of the last
Venus transits. (The pictures above and the proposal for the table below, we
get from another transit project in
Switzerland.
|
| 1st contact
UT[hh:mm:ss]
| 2nd contact
UT[hh:mm:ss]
| 3rd contact
UT[hh:mm:ss]
| 4th contact
UT[hh:mm:ss]
|
| perhaps now
|
|
|
|
|
| probably just now
|
|
|
|
|
| probably over
|
|
|
|
|
| shurely over
|
|
|
|
|
- Using these formulas it will be possible to calculate the relative
parallax angle f for different observers to
arbitrary times:
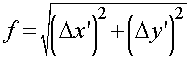
- To get the absolute parallax effect we must know the angular radius
ρS of the sun's disc in absolute terms (e.g. in
arcminutes):
Δβ = f ρS
We will try to get our own measures for ρS (see
project 4).

|
| 
|
| Horizontal view from Essen
|
| Equatorial view from Essen
|
("Horizontal view" means to keep the lower edge of the
picture
horizontal, i.e. parallel to the local horizont, while in the "equatorial
view" the left and right hand sides of the picture are kept parallel to
the celestial north-south-direction.)
Other Mercury Transit Sites:
On each of these sites you will find further useful links.
Mercury really did it! (First
impressions and First
Evaluations)
The distance to the Sun determined, for the first time (see the evaluation page) !
By evaluating pictures of the transit of Mercury, we got the following
results:
- piS=7.0" (from own pictures and diagrams)
- piS=8.6" (from professional pictures)
back to the main page


 Prof. Dr. Udo Backhaus
Prof. Dr. Udo Backhaus
last modification: March 28th, 2008
 Essen, horizontal view
Essen, horizontal view
 Essen, equatorial view
Essen, equatorial view
 Essen, horizontal view
Essen, horizontal view
 Essen, equatorial view
Essen, equatorial view






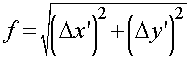




 Prof. Dr. Udo Backhaus
Prof. Dr. Udo Backhaus