 |
 |


We will try to determine the size of the Solar System by measuring the distance of a nearby minor planet (asteroid).
The project aims at determining the distance to the Sun, expressed by means of the Sun's parallax. That is the angular size of the Earth's radius when seen from the Sun, normally expressed in arcseconds. The smaller this angle is, the larger is the distance. The parallax is inversely proportional to the distance.
We are looking for Astronomy On-Line groups interested in parallax measurements by means of CCD imaging. If it will be possible to establish a collaboration with several other groups, preferably at quite different locations on the Earth, we expect to become able to determine the asteroid's parallax and from this to deduce the distance to the Sun.
The current version of this document is not entirely complete, and a few items will be added as soon as possible. Nevertheless, we have felt that it is important that contacts are made already now with other interested groups.
The radius of the Earth's orbit around the Sun is one of the most fundamental constants in astronomy: the Astronomical Unit (AU). Its value is the basis, not only for determing the dimensions and structures of space, but also for measuring the astrophysical properties of planets and stars.
Its value is the basis, not only for determing the dimensions and structures of space, but also for measuring the astrophysical properties of planets and stars.
Because of the rather large size of the AU, all related astrometrical effects, when measured from the Earth, are comparatively small. For this reason the measurement of the Astronomical Unit is very difficult and it was one of the main problems of astronomy over hundreds of years. Up to now there it has never been possible for school students to determine it by means of their own measurements. This is a very challenging project which may now succeed within the framework of Astronomy On-Line!
Because the expected effect is in the range of some arcseconds (for an asteroid with a distance of approximately 1 AU), it will be necessary to take pictures with CCD cameras and telescopes with the longest available focal lengths.
We will offer the Pascal source code of a simple program which calculates the Sun's parallax by combinating two different positions of the asteroid taken simultanously at different observatories or at different times of the same night at the same observatory, respectively.
We hope the result of this cooperation will be a quite good value of the Astronomical Unit, expressed as a multiple of the Earth's radius and therefore in kilometres. Typical pictures and evaluations will be published as soon as possible after the measurements in the "hot phase" of Astronomy On-Line.
During the 18th and 19th century, many expeditions were undertaken to all regions of the world from where astronomers hoped to be able to observe one of the transits of the planet Venus across the Sun's disc - a very rare event. By means of these observations they hoped to get a better measure of the Sun's distance.
Why did different governments spend a lot of money for this? Why did astronomers undergo the hardships during such expeditions? And why is it important even today to know not only the value of the Astronomical Unit, but also something about the methods by which astronomers found it?
We think there are several main reasons:
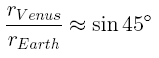
Take a sheet of paper, draw the Sun and the circular orbits of Venus and Earth around it: When the angular distance between the Sun and Venus is at maximum, the line of view from the Earth to Venus is tangential to Venus' orbit, thus forming a right angle with the radius Sun-Venus!) The distance between Sun and Venus is thus about 70 percent of the radius of the earth's orbit.
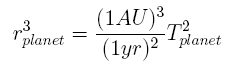
But by all these methods astronomers got the distances as multiples of the radius of the Earth's orbit - and this unit was not well known! An increase (magnification) of the first value by the factor two would have yielded the same magnification of the whole solar system. And the ancient value for the Sun's distance was wrong by a factor of about 20!

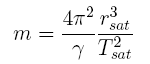
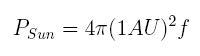
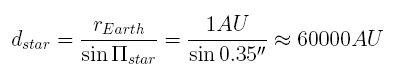
Therefore the distance between the Earth and the Sun is not only a measure of the size of the Solar System (and for the mass of its members for instance), but also for the dimensions of space. For this reason it is called the Astronomical Unit.
By reading about the Astronomical Unit and the development of the interest in its value and the increasing refinement of the methods of its determination, you will learn something about "what it means to do physics and astronomy" and "how it it is possible to know those things" (Wagenschein).
Until the middle of the 16th century, most of the astronomers were not very interested in knowing the exact value of the Sun's distance, because it was just one astronomical distance among many others. This fact was due to the geocentric system of the world that did not allow to deduce the radii of the other planet's spheres from that of the Sun's sphere. Therefore the result of the Greek astronomer Aristarchus, too small by a factor 20, was uncritically taken over by other scientists during nearly two thousand years.
Things changed completely with the development of the heliocentric system by Copernicus: Now the size of the Sun, calculated by its distance, became an important argument for its central position in the planetary system. As described above, it is possible to determine all distances between the planets as multiples of the distance between the Earth and the Sun. Furthermore it became clear that the stars must reflect the Earth's motion around the Sun. But no parallactic motion of the stars could be observed and thus the farther away the Sun would be, the larger would be the distances of the stars. This is why from the beginning of the 17th century increased efforts were made to measure the Sun's distance.
Already the first attempt by Kepler who tried to measure the parallax of Mars at the time of its opposition (when it is placed directly opposite to the Sun, as seen from the Earth) without using a telescope proved the ancient value to be too small by at least by a factor of three. But it took another 70 years before it became possible to measure the Sun's distance by observing a parallactic effect (displacement on the stellar background when observed simultaneously from two or more locations on the Earth) in the position of a planet - Cassini and Richer observed the position of Mars from Paris and Cayenne simultaneously. Due to this important result, the Solar System was now known to be about twenty times larger than what was believed until the time of Kepler!
But the measurements were very difficult and it took another 200 years until the Astronomical Unit was known with an accuracy better than one percent. Therefore it is not surprising that until our days no school experiment has ever attempted to measure it and very few pupils or students know the way astronomers found the correct value.
Even today, the best method of measuring the distance of a distant astronomical object is to determine its trigonometric parallax. You know the underlying effect from everyday life: When you move by bike, car or train, all things around you seem to move in the opposite direction - the nearer they are, the more quickly they move. You will find an excellent description of the method of parallax measurement in the Astronomy On-Line project on the Solar Eclipse on October 12, 1996.
If one tries to measure the sun's parallax in this way, this implies that you must measure its position in the sky from different places on the Earth. In fact, you will have to measure angles in a triangle with a ratio of length of about 24.000:1. Try to draw such a triangle and you will be able to imagine the corresponding difficulties! Indeed, up to now it is impossible to measure the Sun's parallax in this way directly.
There are three principal alternatives:
We think that it would be fascinating to be able to do and to understand the measurement of an astronomical constant, with such a long history, during which the problem contributed to the advancement of the development of astronomical theories, methods and instruments.
Among the above methods, the idea of Aristarcos can be understood most easily. But, unfortunately, it has proven impossible to realize it, even by using a sextant (see, for instance, D. Vornholz, U. Backhaus: "Wer hat recht - Aristarch oder der Sextant?" (in German), Astronomie + Raumfahrt 31, 20 (1994)). Therefore, reversing Roemer's method of determing the velocity of light (that means to deduce the radius of the Earth's orbit from the known value of the velocity of light) seems to us to be the only method which can until now be done at schools by their own measurements.
We will now try to realize the early idea of Kepler and the first successful method of Cassini. But we will not observe the planet Mars (it is too far from the Earth at the end of November and because of its size and brightness, precise measurements of its position would be too difficult). Instead of Mars we will use a minor planet which is opposite to the Sun and therefore relatively close to the Earth (1 AU approximately) and can be observed during the entire night.
Having looked for such asteroids by using Dance of the Planets and Guide 4.0 respectively we found the following minor planets which seem to us to be appropriate: 84 Klio, 584 Semiramis and 990 Yerkes. We think that 4179 Toutatis will be too close to the Sun and of too faint magnitude. Ephemeris data of these asteroids are given in a separate paper.
We are going to measure the distance of the minor planet by means of the parallax method. The principles of this method are excellently described in the solar eclipse project of Astronomy On-Line.
Because of the distance of the asteroid, the corresponding parallax effect will be small (less than 8 arcsec approximately). To achieve the required accuracy we will therefore use CCD imaging.
A topocentric" position of a celestial object means that the position is measured from a real (topocentric) location on the Earth, for instace from an observatory. This is different from a geocentric position, which refers to the hypothetical position of the object, if it were observed from the Earth's center.
To be able to determine the exact position of the asteroid from a picture, it must show besides of the asteroid at least three stars with known positions. For this purpose, we will use the astronomy program Guide 4.0 and its Guide Star Catalogue.
From these equatorial positions and the corresponding pixel positions we can calculate the so called plate constants of the picture (see, for instance, O. Montenbruck et al., Astronomy on the Personal Computer, Springer, 1994). From these constants it is possible to determine the equatorial coordinates of the asteroid very precisely. We will do this by means of the astrometry programs MiPS and MIRA respectively.
The result of this first step of evaluation will be the exact topocentric equatorial coordinates of the planet:
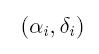
The two topocentric positions of the asteroid give us the directions of view due to the corresponding observers, and leed us to the following situation:
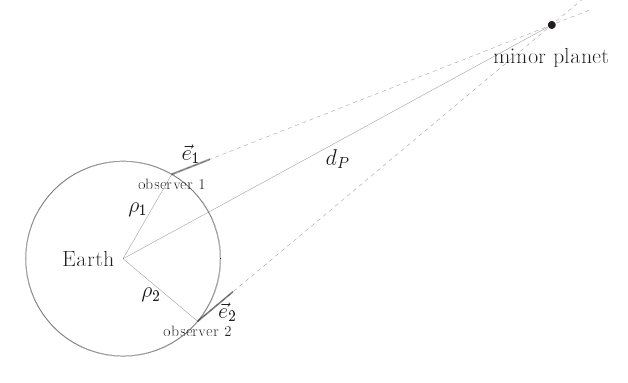
Therefore, by determining the intersection of the respective lines of view, we are able to calculate the distance dP between the asteroid and the Earth's center. The details of this calculation are given in a separate document. We get this distance as a multiple m of the Earth's equatorial radius rE:
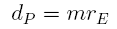
If the orbital elements of the asteroid are known, it is possible to determine its geocentric distance as a multiple n of the Astronomical Unit by means of ephemeris data calculation:
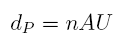
It should be stressed that for this calculation it is not necessary to know the absolute value of the Astronomical Unit!
The combination of the two equations above then give us the Astronomical Unit as a multiple of rE:
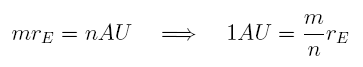
Thus, if we know the Earth's radius in kilometers (and we do!) we will find the Astronomical Unit in the same measure.
Most often the Sun's distance is given as the Sun's parallax. That is the angular size of the Earth's radius when seen from the Sun (or, vice versa, half of the maximum parallax effect of the Sun observed from the Earth). This angle can easily be calculated.
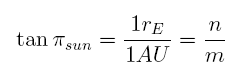
For very small angles, the tangent is very nearly equal to the angle itself expressed in radiants. Thus, the last step we have to do is to convert the parallax into arcseconds:
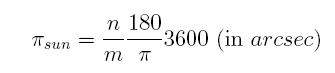
Instead of communicating with another observatory, we can in principle take advantage of the Earth's daily rotation to 'move' to a place with another equatorial position. Unfortunately, this takes some time and during this time the asteroid will not remain in a fixed position! But we will be able to take into account its proper motion, at least approximately.
An ephemeris calculation gives us not only the geocentric distance of the asteroid but its geocentric equatorial coordinates. We use these geocentric positions at the respective times of observation:
to determine the proper motion of the asteroid. By this we can reduce the topocentric position due to the second observation to the time of the first one.
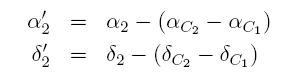
By this `trick' we have obtained two observations which refer to the same time but with different positions of the observer! Therefore, we can now calculate the Sun's parallax in exactly the same manner as we did above.
It is even possible to calculate the Sun's parallax with only one observed topocentric position of the asteroid.
For this purpose we take the geocentric position we got by means of ephemeris data calculation as the second "topocentric" position of the asteroid. Thus, by `locating' the `second' observer in the Earth's center and setting
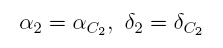
we can use the same algorithm as for two real observer positions.
By the third method we combine an observed position with a theoretical one. We, therefore, do not really measure the Sun's parallax. Furthermore, we need a highly precise geocentric position. For this reason, this method is very sensitive to numerical errors of the ephemeris data calculation.
For the second method we do not really need the exact geocentric positions, but only the proper motion of the asteroid as viewed from the Earth's center. This motion is influenced by the other planets much less than its exact position (in which the perturbations are cumulated). That means that a simpler method of calculation may be used. To be more specific, if we begin with good orbital elements, it is sufficient to take into account only the influence of the Sun. For this reason, this method is less sensitive and appropriate algorithms of calculation can easily be found.
Finally, the first method determines the asteroid's distance from two observed positions only. It use ephemeris data calculation only for deducing the Sun's parallax. For this only the geocentric distance of the asteroid is needed which can easily be calculated with sufficient accuracy. Moreover, this calculated value only influences the final result in a linear way. Therefore, this method is much less sensitive than the others. For this reason, we would by far prefer to determine the Astronomical Unit from two positions observed from two different observatories!
The pictures at the top of this document were taken by us in collaboration with Erwin Heiser, member of the Astronomische Arbeitsgemeinschaft Osnabrück at the observatory on the Oldendorfer Berg. They show the minor planet 84 Klio at October 14, 1996 (ephemeris data of this asteroid and some others are contained in a separate paper). They were taken at 19:16:57 UT and 20:10:01 UT respectively. In spite of the short time interval, they clearly show the proper motion of Klio!
An evaluation of these pictures is described separately.