 Essen, horizontal view
Essen, horizontal view
Internet Project
Observing, Photographing and Evaluating the
Transit of Venus, June 8th, 2004
 Essen, equatorial view
Essen, equatorial view
 Essen, horizontal view
Essen, horizontal view
|
Internet ProjectObserving, Photographing and Evaluating theTransit of Venus, June 8th, 2004 |
 Essen, equatorial view
Essen, equatorial view
|
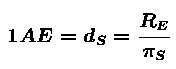
For this reason, you may contact other participants of our project who are suitably located with respect to your own site.
Because there are other collaborative projects which have been executed in the past and the material of which can still be found in the internet (see, for instance, the Erathostenes project and its final report) the basic idea and some methods of measurement are described here only shortly.
For these observers, it is not necessary to use a clock. Both of them measure the length lS of the shortest shadow of a vertical pole of length l. In that moment it is local noon, that means the Sun culminates. Than, the angles zi can easily be calculated from the ratio lS/l.
The central angle and the Earth's radius can than be calculated as shown in the left picture above.
For these observers, it is crucial to have synchronized clocks because they must exactly measure the time at which the length of the shadow of a vertical pole is at its minimum. As, around the time of culmination, the length of the shadow is changing only slightly it is better to determine the time of the shortest shadow by the method connoted in the picture below:
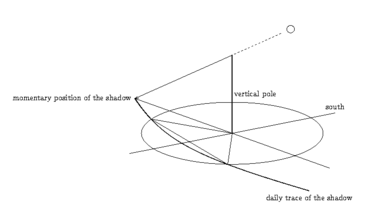
The direction to south determined in this way should be marked as exactly as possible. It is the basis not only for position measurements on Earth but also for precisely locating the Sun and determing the sideral time (project 2)!
The central angle which is, in this case, located not at the Earth's center but at the axis of rotation, and the Earth's radius can than be calculated as shown in the right picture above. The geographical latitude must be known.
In both cases, the distance between the observers along the Earth's surface must be known. Usually, it will be taken, for instance, from a map. Nevertheless, it would be more satisfying to determine that distance by an own trip but that is possible only for short distances. But in that case, one has to measure the length of the shadow very precisely.
If you use a pin hole instead of the tip of a stick it is possible to reduce the error to about 0.1 degree. Than, you may be able to measure the distance by bike: The angle belonging to a trip of 30 kilometers is about 0.25 degree.

|
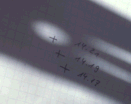
|
|---|---|
| Pinhole and pendulum serve as a vertical pole. | The pinhole generates an elliptic picture of the Sun whose center can be located very precisely. |
| Measuring the exact of local noon ... | |
|---|---|
 |
 |
| ... in Essen | ... in Isfahan |
cos η = sin λ1 sinλ2 + cosλ1 cos λ2 cos(φ1-φ2) = 37.9°

 Prof. Dr. Udo Backhaus
Prof. Dr. Udo Backhaus